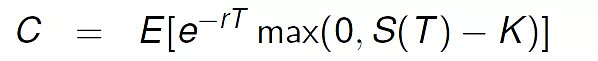金融市场上的衍生品大可分为四类：远期forwards、期货futures、期权options和互换swaps。

其中期权最为复杂，原因是难在定价上。首先从本身的定义规则来看，期权代表的是行使未来某一时刻的权利，它不像其他金融衍生品必须履行某种契约，所以给权利定价就变得抽象且复杂。如果从数学的角度看，给权力定价则变成了计算某个公式，以欧式看涨期权为例，就是计算下面的公式：

看起来就一行也不长，但手算还是需要花些时间的。

而电脑的出现恰好解决了时效的问题，所以接下来本文将介绍Python编程语言中的quantsbin程序包来完成对期权的定价。

在编程开始之前，首先对期权的定义进行一些简单介绍。

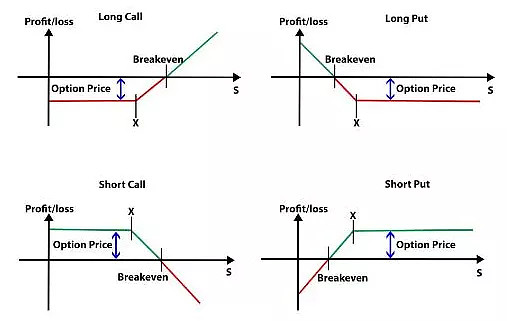
期权可分为看涨期权（call option）与看跌期权（put option），每一个又可以采取做多或做空的策略，所以一共有四种情形，很多人容易对这四种情况混淆，在这简单总结一下：

做多看涨期权long the call：价格上涨后能低价买。

做空看涨期权short the call：对方要求低价买，所以只好低价卖。

做多看跌期权long the put：价格下跌后能高价卖。

做空看跌期权short the put：对方要求高价卖低价的东西，只好高价买。

用收益图比较来看，就更清楚一点：

这是按游戏规则来划分的，如果按行权时间来分类，则分为欧式期权、美式期权和百慕大期权。

欧式期权只有一个行权日，即到期日。美式期权则可以在到期日之前任意时间行权，而百慕大期权介于欧式与美式之间，在到期日之前的特定几个日期可以行权。

以上就是关于期权一些浅显的知识，了解这些后可以更好地理解后面的计算。

相比于其他金融产品的期权，欧式股票期权应该是最简单的了，我们就从最简单的开始入门。

比如，某股票目前的价格在29块每股，如果买入一看涨期权，到期日为半年后，可以以30块每股的行权价格买入，那目前此期权价格应该是多少呢？

（假设年化无风险利率为5%，此股票年化波动率为10%）

首先我们需要安装及导入相关的程序包quantsbin：

# 安装

pip install quantsbin

# 导入

import quantsbin.derivativepricing as qd

接下来输入计算的方程，

equity_option = qd.EqOption(

option_type = "Call",

expiry_type = "European",

strike = 29,

expiry_date = "20200501")

equity_option_v = equity_option.engine(

model = "BSM",

pricing_date = "20191201",

spot0 = 30,

rf_rate = 0.05,

volatility = 0.1)

# 计算

equity_option_v.valuation()

1.952928350088847

其中第一行EqOption是股票期权的内置方程，参数包含：

option_type：期权类型【“Call”，“Put”】

expiry_type：行权类型【“European”，“American”】

strike：行权价格

expiry_date：到期日【“YYYYMMDD”】

第二个方程用于输入计算参数：

model：计算模型【BSM：black-scholes-model，MC_GBM，Binomial】pricing_date：当前日期【“YYYYMMDD”】

spot0：当前股票价格

rf_rate：年化利率

volatility：年化波动率

最后一行便是计算出的最终期权价格，结果为1.952。

为了验证准确性，我用Black-Scholes模型公式再重新计算一下：

import numpy as np

import pandas as pd

import scipy.stats as sci

def call(S,K,T,rf,sigma):

d1 = (np.log(S/K)+(rf+0.5*sigma**2)*T) \

/(sigma*np.sqrt(T))

d2 = (np.log(S/K)+(rf-0.5*sigma**2)*T) \

/(sigma*np.sqrt(T))

c = S*sci.norm.cdf(d1)-\

K*np.exp(-rf*T)*sci.norm.cdf(d2)

return c

call(30,29,0.5,0.05,0.1)

1.9494474031880422

结果计算出来为1.949，与quantsbin程序包计算出来的1.952十分接近，说明quantsbin程序包计算出来的数据大致准确，可以使用。

此外，我们还可以计算相应期权的希腊值：

print(equity_option_v.risk_parameters())

{'delta': 0.8073646985204345, 'gamma': 0.12883104682859778, 'theta': -0.00463889968525322, 'vega': 5.813280387032892, 'rho': 11.165092460993892, 'phi': -12.143649848978592}

由于美式期权的行权时间不是固定的，就导致数学计算上相当复杂，相比之下，用蒙特卡尔或二叉树的方法来计算价格会更方便一些，而quantsbin程序包里正有这些。

为了把欧式与美式两者进行比较，下面先是欧式期权的计算，与上文有同样的参数，其中多加了一项yield_div，代表股息收益率。

equity_option = qd.EqOption(

option_type = "Call",

expiry_type= "European",

strike = 29,

expiry_date = "20200601")

equity_option_v = equity_option.engine(

model = "BSM",

pricing_date = "20191201",

spot0 = 30,

rf_rate = 0.05,

volatility = 0.1,

yield_div = 0.02)

# 计算

equity_option_v.valuation()

1.7161326885968933

下面是美式的计算：

e_Aoption = qd.EqOption(

option_type = "Call",

expiry_type= "American",

strike = 29,

expiry_date = "20200601")

e_Aoption_v = e_Aoption.engine(

model = "Binomial",

pricing_date = "20191201",

spot0 = 30,

rf_rate = 0.05,

volatility = 0.1,

yield_div = 0.02)

e_Aoption_v.valuation()

1.7174828307248409

运行后出来的结果显示，欧式看涨期权价格在1.716，美式则为1.717，美式的比欧式的价格略高，不过近乎一样，这是由于时间价值。所以一般看跌期权，两者之间的差距会更明显。

以标的资产为汇率的期权就是汇率期权（Forex option）。

标准的欧式汇率期权数学公式可写成：

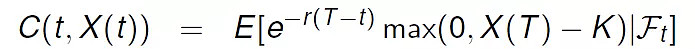
比如目前1欧元可以换1.11左右美元，一年后可以按1：1.20的比例换美元的期权价格应该是多少？假设EUR/USD汇率的年化波动率为15%，欧元年化利率0.1%，美元年化利率4%，我们可以写入以下代码：

EUR_USD = qd.FXOption(

option_type = "Call",

strike = 1.2,

expiry_date = "20201201",

expiry_type = "European")

EUR_USD_Op = EUR_USD.engine(

model = "Binomial",

spot0 = 1.11,

pricing_date = "20191201",

volatility = 0.15,

rf_rate_local = 0.04,

rf_rate_foreign = 0.001)

EUR_USD_Op.valuation()

0.04809404656589679

得到的结果为0.0481，再用汇率期权的数学公式计算一下，看是否一样：

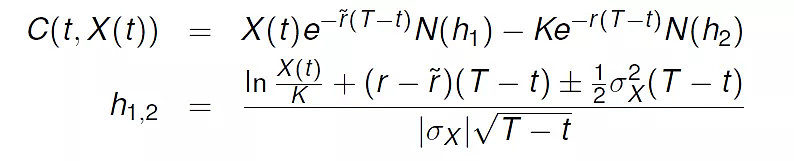
def FXcall(S,K,T,r,rf,sigma):

d1 = (np.log(S/K)+ \

(r-rf+0.5*sigma**2)*T) \

/(sigma*np.sqrt(T))

d2 = (np.log(S/K)+ \

(r-rf-0.5*sigma**2)*T) \

/(sigma*np.sqrt(T))

c = S*np.exp(-rf*T)*sci.norm.cdf(d1)- \

K*np.exp(-r*T)*sci.norm.cdf(d2)

return c

FXcall(1.11,1.2,1,0.04,0.001,0.15)

0.04784737572960368

公式计算出的结果是0.0478，与0.0481非常接近了。

商品期权跟股票期权不用的是，商品期权没有股息收益（dividend yield），但是存在convenience yield和cost yield两项。

假设目前黄金现货价格在1300美元每盎司，一年期的看跌期权，行权价格在1200美元的期权价格是多少，并假设波动率为0.3，美元利率0.04，convenience yield 0.03，cost yield 0.02，可写入以下代码：

gold = qd.ComOption(

option_type = "Put",

strike = 1200,

expiry_date = "20201201",

expiry_type = "European")

gold_Op = gold.engine(

model = "Binomial",

spot0 = 1300,

pricing_date = "20191201",

volatility = 0.3,

rf_rate = 0.04,

cnv_yield = 0.03,

cost_yield = 0.02)

gold_Op.valuation()

88.3944411947053

以上就是几种常见期权的定价过程，其实期权下细分还有很多不同的种类，比如其中一种叫做奇异期权（Exotic option），正如像其名字那样，规则上五花八门、乱象奇绝，所以不像上面介绍的几种有统一的定价公式可以直接计算，这时就需要按其自身定义的游戏规则，编写相应的方程来计算得出。

更多内容请参考quantsbin官网文件：网页链接